Experimental 12-TET: Part 2

Last time we looked at equal tempered systems and how they are always of the form:

And then we explored how we could choose alpha such that we could make certain intervals, such as the 5th, nice. But the problem was that making one interval nice would make others worse than 12-TET. So how can we choose alpha such that we get as close as possible to all the intervals?

Linear regression

The basic idea of linear regression can be summed up in this picture:

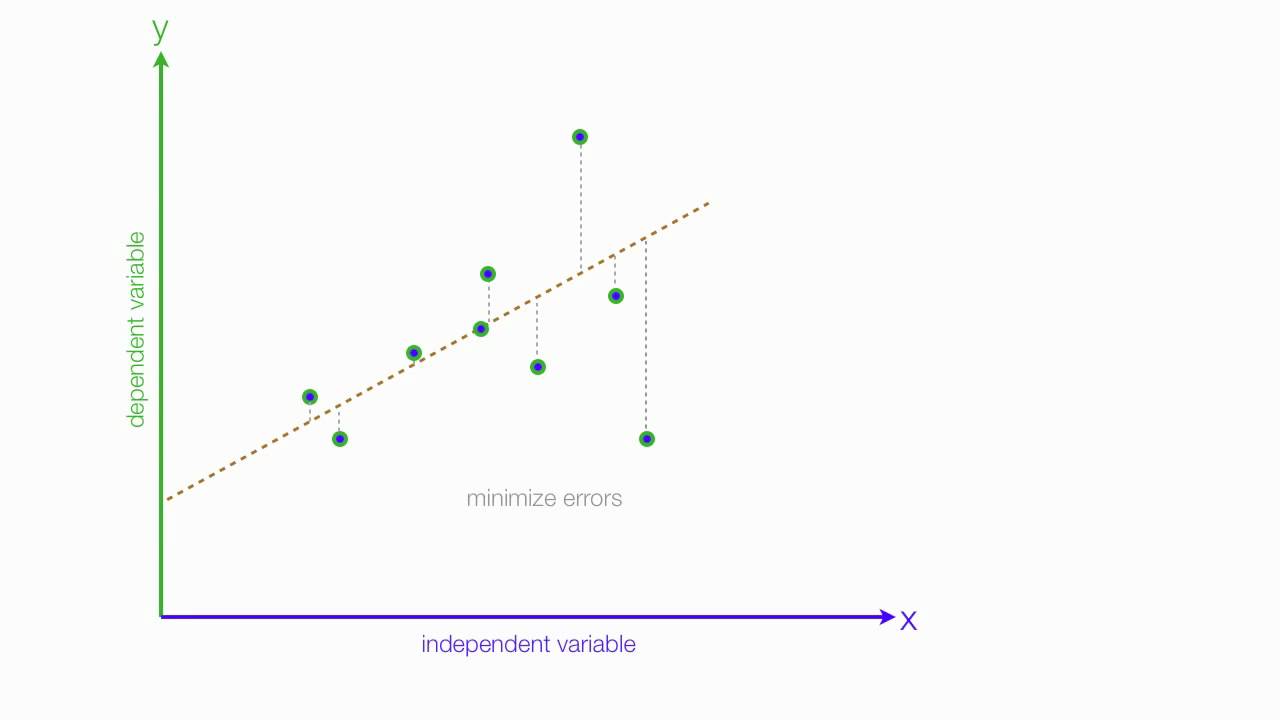
Essentially, it’s a mathematical algorithm to draw line that best fits the data. So, for a given series of data paired with it will find a and b so that . There are more technical details of this algorithm that I won’t go into.
Now looking back at our equation(let’s just say K=1 since it’s not important here):

Take logs on both sides:

Now, since we chose K=1, then T(n) will be the ratio of the nth interval. For example, T(7) is the ratio of the 5th, which should be 1.5. In fact let’s make our ideal frequency ratio’s(e.g. ) then we can use our regression algorithm on and n which will find the value of which minimises our error.
OK so if we do that we get and therefore our magic value of alpha is:
1.059234861
I call this tuning “DK-Tuning” as it’s the only tuning worthy of our lord and saviour.

It’s is actually very close to 12-TET. I only did this for 1 octave, but if you did this for infinitely many octaves you would get exactly the same alpha value as normal 12-TET, since the interval ratios double every octave and any other value will slowly drift away from these octaves.

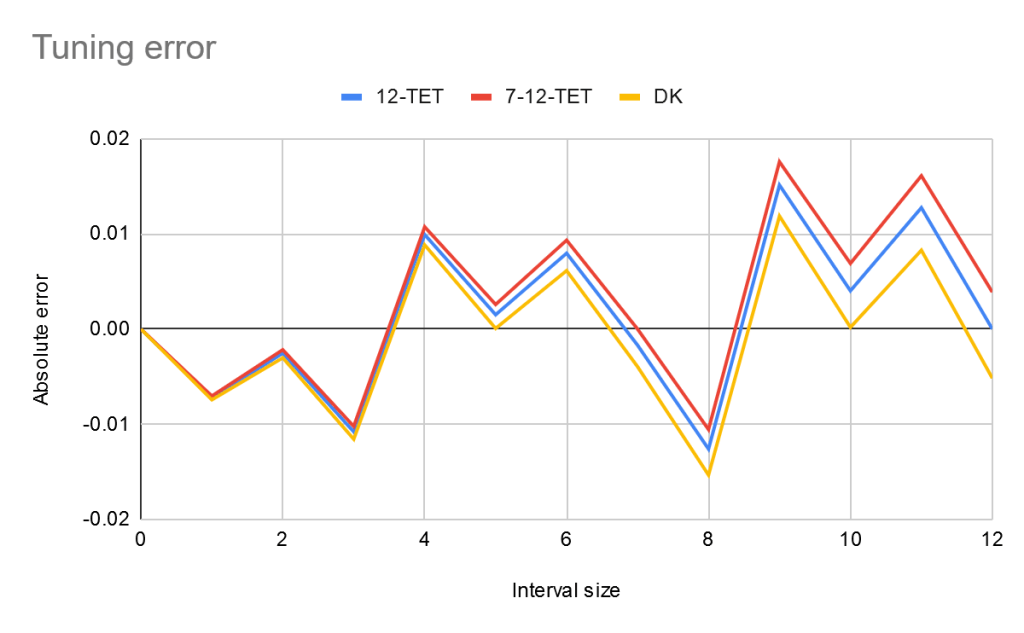
DK vs 12-TET

OK now for the comparison, this time in the form of a graph:

And now an audio comparison, try listening first before checking the order and decide which one you like best:

So what did you think? It’s pretty hard to tell the difference but 12-TET was second and DK was first.

Try it yourself

As before, these weird tunings(and more!) can be tried on my VST: https://github.com/AugsEU/Augs-Synth